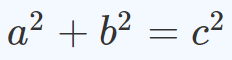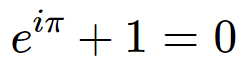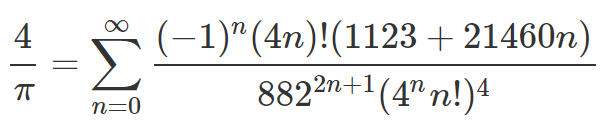世の中には数学の公式が山ほど存在しているが、その中で個人的に美しいと思ったものを紹介したい。
最初の2つは誰もが知っている数式だと思う。
そして、最後の式は別次元だ。
数学史上最高の天才との声もあるインドの数学者が生み出したものである。
ピタゴラスの定理
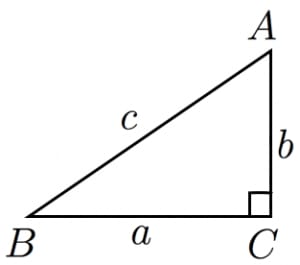
3位 ピタゴラスの定理
下図のような直角三角形
において、
が成り立つ。
ピタゴラスの定理は、誰しもが知ってる直角三角形の辺の長さの関係を表す公式である。
この定理は、数学だけでなく物理をはじめあらゆる分野で活躍する応用範囲の広さもさることながら、証明方法も数多くあり長く楽しめる数式であることも高ポイントである。
オイラーの等式
2位 オイラーの等式
これに関してはもはや説明不要であろう。
美しい数式としてほとんどの人がまず挙げるのがこのオイラーの等式である。
e:ネイピア数
i:虚数単位
π:円周率
これらの基本的な数学定数がとんでもなく簡潔に結び付けられる。
これほどパッと見て美しいと言える式はないだろう。
ラマヌジャンの円周率の公式
1位 ラマヌジャンの円周率の公式
最後は、恐怖にも似た美しさを持つラマヌジャンが発見した円周率の公式である。ラマヌジャンは1887年にインドで生まれた数学者だ。
この数式もまずは何も言わずに見てほしい。
これが、インドの魔術師と呼ばれた天才ラマヌジャンの世界である。
どうだろう、何かとてつもない恐怖を感じないだろうか。
僕はこの式を初めて見たとき、思考が前に進まなかった。
まず、この式を証明したいがどこから手を付ければよいか全くわからない。
1123、21460、882って数はどこから出てきたの?
何このぐちゃぐちゃな式。
人間が作れるものなの?
見た人に色々な感情を植え付けさせられる式である。
しかもすごいのは、この式は円周率に収束するスピードがめちゃくちゃ速いという有効性も持ち合わせていることだ。nを少し増やしただけで円周率πにかなり近づくため、高精度な円周率を高速に求めることができる。
しかし、一番すごいのはやはりこの式を発見したラマヌジャンであろう。
ラマヌジャンに関しては、とんでもないエピソードが数多く残っている。
ラマヌジャンは100点
19世紀後半から20世紀にかけて活躍したイギリスの数学者、ゴッドフレイ・ハロルド・ハーディ(この人も偉大な数学者)は数学者に1から100までの点数をつけていた。ハーディの評価は、
「自分は25点、リトルウッドは30点、ヒルベルトは80点、ラマヌジャンは100点」であった。
注:リトルウッドとヒルベルトもとんでもなく偉大な数学者である。
夢の中で公式を作った
ラマヌジャンはこのような公式をどうやって発見したのか。ラマヌジャン自身はこう答えたらしい。
「寝ている間にナーマギリ女神が教えてくれた」
全て寝ている間に思いついたわけではないと思うが、ちょっと引くほど恐ろしい回答である。
自分が数学者を目指していて、友達がこんなことを言ってラマヌジャンの様な公式を見せてきたら、もう数学で勝てる気がせずやる気をなくしてしまうかもしれない。
こいつは本当に同じ人間なのか?
そう思わせる恐ろしいエピソードである。
ラマヌジャンがいなかったらこの式は発見されてない
ラマヌジャンが発見した公式は、数学者でも発見に至る思考をたどることが難しい。
普通の数学者とラマヌジャンの見ていた世界があまりにも乖離していたため、
「相対性理論はアインシュタインがいなくても数年以内に誰かが発見しただろうが、ラマヌジャンの見つけた公式は彼が死んで100年経った今でも誰も発見できなかっただろう」
と言われている。